Constraint Satisfaction for Christmas

October 27, 2024 - 10 min read

How do I prevent my coworkers from hating me?

Many years ago, I faced the challenging task of dividing on-call duties during the holidays. Luckily, Constraint Programming provided a fair solution.

What is on-call

Software engineers often have on-call responsibilities outside of working hours. The on-call engineer is responsible for responding to alerts from the company’s incident management software. These alerts can be noisy and disruptive. I have been woken as early as 2 am to resolve complicated technical problems.

As humans, software engineers want to avoid unnecessary on-call shifts as much as possible. Deciding who will need to miss time with their family to respond to alerts, can become fairly contentious. This is especially true over the winter holidays.

The Requirements

During the holidays, we need to ensure fairness in scheduling. I had the following requirements dictated to me:

No engineer can be on-call on consecutive days
No engineer can be on-call more than 7 days total
No engineer can be on-call less than 5 days total
No engineer can be on-call on a day they are absolutely busy on
No engineer can be on-call for more than one major holiday
- Thanksgiving, Xmas, etc

Given these, it is possible to manually divvy up the days between all the engineers on the team. However, this might introduce bias (percieved or otherwise). We need a way to automate the process.

Constraint Satisfaction

In mathematics and computer science, there exists a class of problems focused on finding solutions to a set of constraints. We call these Constraint Satisfaction Problems (or CSP). CSPs consist of variables (what we need to assign), domains (the possible values for each variable), and constraints (the rules that must be followed). There are many examples of CSPs (Sudoku, Crossword Puzzles, etc). Let’s define these more rigorously:

\begin{equation} \begin{aligned} X = \{ X_{1}, \ldots, X_{n} \}\\ D = \{ D_{1}, \ldots, D_{n} \}\\ C = \{ C_{1}, \ldots, C_{m} \}\\ \end{aligned} \end{equation}

Sudoku is a good example of a CSP. We can think of the variables as the 9x9 grid. The domains are all the numbers that could possibly be placed in each square (the given squares would have a domain of just that number). Finally, the constraints are the 3 basic rules for sudoku:

Unique numbers in each column
Unique numbers in each row
Unique numbers in each subgrid

That’s all that’s needed to set up the problem. There are many simple and complicated puzzles that will fit this framework. But, how do we actually solve these problems? While there are a few different approaches, we will be using the simplest: Backtracking.

Backtracking

Imagine we need to color a list of items so that no two adjacent items share the same color. This might look like the following:

\textcolor{red}{\bullet} \textcolor{blue}{\bullet} \textcolor{red}{\bullet} \textcolor{blue}{\bullet} \textcolor{red}{\bullet}

For simplicity sake, let’s limit our problem to only 3 items. We can update our previous equations based on the new premise.

\begin{equation} \begin{aligned} &X = \{ \textcolor{gray}{\bullet}_{1}, \textcolor{gray}{\bullet}_{2}, \textcolor{gray}{\bullet}_{3} \}\\ &D = \{ [\textcolor{red}{\bullet}, \textcolor{blue}{\bullet}], [\textcolor{red}{\bullet}, \textcolor{blue}{\bullet}], [\textcolor{red}{\bullet}, \textcolor{blue}{\bullet}] \}\\ &C = \{ AdjColorDiff \} \end{aligned} \end{equation}

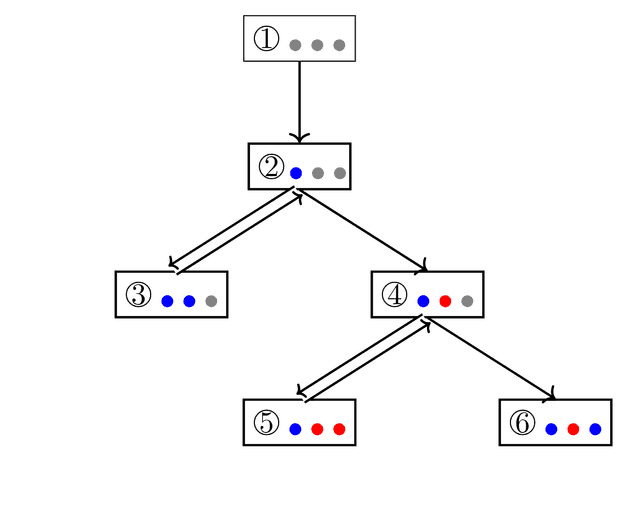
Just like a child finding their way through a maze, we are going to come across many forks in the path. By randomly making a choice, we may evantually find ourselves at a dead end. When this happens, we will backtrack to the last choice we made and make another. If we run out of choices, backtrack again and repeat. Evantually, we will find the path to the maze’s exit. This is essentially how we are going to solve CSPs. Instead of dead ends in the maze, our algorithm will check if any of the constraints are broken. If they are, we can backtrack and try a different path.

In the above graph, we can see how our algorith solves the coloring problem. If we follow the numbers on each node, along with the arrows, we can see how the backtracking algorithm will evantually come to a correct solution.

While this is a very simple problem, easily solvable by a child, the key is that we can apply this same algorithm to any CSP and implement it in code. I have defined a python script that can help us solve any CSP:

class CSP:
    def __init__(self, variables, domains, constraints=[]):
        self.variables = variables
        self.domains = domains
        self.constraints = constraints
        self.solution = None

    def solve(self):
        assignment = {}
        self.solution = self.backtrack(assignment)
        return self.solution

    def backtrack(self, assignment):
        # Base case - no unnasigned variables left
        if len(assignment) == len(self.variables):
            # Run constraint checks one last time
            for var in self.variables:
                if not self.checkConstraints(var, assignment[var], assignment):
                    return None
            return assignment

        var = self.findUnassignedVar(assignment)
        for value in self.getDomainVals(var, assignment):
            if self.checkConstraints(var, value, assignment):
                assignment[var] = value
                result = self.backtrack(assignment)
                if result is not None:
                    return result
                del assignment[var]
        return None

If you are unfamiliar with Python, the above code simplify translates my english description of backtracking into actual executable instructions. You may notice that no where in the above code do we reference colors or any other aspect of the problem. That’s because the code abstracts away those implementation details. We can solve the coloring problem with a very simple python script:

from csp import CSP

variables = [i for i in range(3)]
domains = {var: ['Red', 'Blue'] for var in variables}

# Check that no element neighbors the same color
def neighborConstraint(var, value, assignment):
	# Check left neighbor
	if var - 1 in variables:
		if var - 1 in assignment and assignment[var - 1] == value:
			return False

	# Check Right neighbor
	if var + 1 in variables:
		if var + 1 in assignment and assignment[var + 1] == value:
			return False

	return True

# Constraints
constraints = [
    neighborConstraint
]

print("*"*7, "Solution", "*"*7)
csp = CSP(variables, domains, constraints)
sol = csp.solve()

# Blank Solution
solution = ['' for i in range(3)]
for i in sol:
	solution[i] = sol[i]

print(' '.join(solution))

The beauty of this approach is that the same code can be used for any number of puzzles and games. In addition to the coloring problem, I have also created solvers for the 8-Queens Problem and Sudoku. You can find all the code I have written for this blog post on github.

Back to Scheduling

So how does this look like in practice for scheduling on-calls for the holidays? I am going to break down the code to hopefully make it easier to follow.

Step 1 - Setup

We have a selection of dates that we need to schedule. For now, let’s list them as follows:

# Variables
variables = [
    "2024-11-28", # THANKSGIVING
    "2024-11-29", # BLACK_FRIDAY
    "2024-12-24", # XMAS_EVE
    "2024-12-25", # XMAS_DAY
    "2024-12-31", # NY_EVE
    "2025-01-01", # NY_DAY
]

We also have a list of people that we need to assign to those days.

# Domains
ALL_PEOPLE = [
    "Alice",
    "Bob",
    "Curtis"
]
domains = {day: ALL_PEOPLE for day in variables}

We’ve just defined our variables and domains. Given just these, we can run our algorithm without any constraints to get a preliminary schedule.

> # Step 1
> print("Step 1 - Set Up")
> csp = CSP(variables, domains)
> sol = csp.solve()
> 
> printSchedule(sol)

Step 1 - No Constraints
**********
{'2024-11-28': 'Bob', '2024-11-29': 'Curtis', '2024-12-24': 'Bob', '2024-12-25': 'Bob', '2024-12-31': 'Bob', '2025-01-01': 'Bob'}
**********

However, this is not very interesting. Alice doesn’t even get assigned a single day! Let’s add some constraints.

Step 2 - First Constraint

First, let’s define a very simple constraint that checks that no one is assigned two days in a row:

# Make sure that the same person is not assigned to two days in a row
def noConsecutiveDaysConstraint(var, value, assignment):
    # First check before the set date
    yesterday = var - timedelta(days=1)
    if yesterday in assignment and assignment[yesterday] == value:
        return False
    # Next check after the set date
    tomorrow = var + timedelta(days=1)
    if tomorrow in assignment and assignment[tomorrow] == value:
        return False
    return True

We can then modify our codebase to include this new constraint:

> constraints = [
>     noConsecutiveDaysConstraint
> ]
...

Step 2 - No Consecutive Days Scheduled
**********
{'2024-11-28': 'Bob', '2024-11-29': 'Curtis', '2024-12-24': 'Curtis', '2024-12-25': 'Alice', '2024-12-31': 'Bob', '2025-01-01': 'Alice'}
**********

This gives us much better results, but our CSP solver allows us to add as many constraints as we want!

Step 3 - Max Days Constraint

We can add yet another constraint that limits the max number of days that any one person can be assigned:

# Makes sure that no one is assigned to too many days
def maxDaysConstraint(var, value, assignment):
    global variables, ALL_PEOPLE
    count = 0
    for day in variables:
        if day != var and day in assignment:
            if assignment[day] == value:
                count += 1
    # Make sure no one is assigned to too many days
    return count <= len(variables) / len(ALL_PEOPLE)

The above code will find all the days that have the same assignee as the given day (var). We constrain the schedule such that noone has more than their fair share of the total number of days. This gives us a fairly good looking schedule:

Step 3 - Max Days Scheduled per Person
**********
{'2024-11-28': 'Alice', '2024-11-29': 'Curtis', '2024-12-24': 'Bob', '2024-12-25': 'Alice', '2024-12-31': 'Bob', '2025-01-01': 'Curtis'}
**********

Step 4 - Unavailability Constraint

We also need to allow for people to opt out of days. If Alice or Charles is not available for Thanksgiving, we need to account for that. I use a fairly complicated bit of python to implement this logic. The following code takes in a map of days to unavailable people and returns a function pointer that matches our constraint interface.

# Takes a map of days to list of people that are unavailable to work
def unavailableConstraint(unavailable):
    def fn(var, value, assignment):
        count = 0
        day = var.strftime("%Y-%m-%d")
        if day in unavailable:
            # Check if person is unavailable to work that day
            if value in unavailable[day]:
                return False
        return True
    return fn

We can then update our list of constraints like so to get a compliant list of results.

> constraints = [
>    ...
>    unavailableConstraint({
>        "2024-11-28": ["Alice", "Curtis"],
>        "2024-12-31": ["Bob"],
>    }),
>]

Step 4 - Unavailable Days
**********
{'2024-11-28': 'Bob', '2024-11-29': 'Curtis', '2024-12-24': 'Bob', '2024-12-25': 'Curtis', '2024-12-31': 'Alice', '2025-01-01': 'Curtis'}
**********

Step 5 - putting it all together

At this point, we have most of the constraints that we listed in the original problem statement. We are only missing the limit of one person per holiday. We also are only using 6 of the 40 days that we need to assign. Let’s expand the problem by adding 3 more engineers, adding all the days we need, and also implementing the last constraint:

# Add more engineers
ALL_PEOPLE += [
    "Doug",
    "Ethan",
    "Frank"
]
variables = generateConsecutiveDates("2024-11-23", "2025-01-01")
domains = {day: ALL_PEOPLE for day in variables}

# Makes sure that no one is assigned to more than 1 major holiday
def onlyOneHolidayConstraint(var, value, assignment):
    # No one should be assigned to more than 1 holiday
    holidays = [
        "2024-11-28", # THANKSGIVING
        "2024-11-29", # BLACK_FRIDAY
        "2024-12-24", # XMAS_EVE
        "2024-12-25", # XMAS_DAY
        "2024-12-31", # NY_EVE
        "2025-01-01", # NY_DAY
    ]

    # Only run constraint on holidays
    if var not in holidays:
        return True

    for holiday in holidays:
        if holiday != var and holiday in assignment:
            if assignment[holiday] == value:
                return False

    return True

At last, we have a piece of code that will actually assign all the engineers on my team to the holiday on-call schedule! You will notice that the underlying CSP implementation is unchanged from our toy coloring problem. We have implemented an abstract CSP solver that can assign engineers as needed. Everyone can rejoice knowing that this solver will handle scheduling without bias.

If you use my code, feel free to experiment with new or modified constraints to fit your needs.

Shortfalls and Future Work

While the solver I provided can find a solution, there are important considerations to keep in mind before using it.

Sometimes there may not be a solution
- Imagine if everyone says they will not be available on christmas
- I avoided this by utilizing social pressure, I made the days everyone was unavailable public via a spread sheet
Overconstrained or Large Search Spaces are innefficient
- There are around $6^{40}$ combinations of schedulings
- There may only be small number of possible solutions, increasing computation time
Randomizing the domain order is important
- I found that shuffling around the domain for a variable before we iterate can both decrease computation time and reduce bias from a static ordering

I also have identified future work that would improve my implementation:

Better Constraint Interface
- I can reduce the total time spent searching by only running certain constraints when they are applicable
- Some of the constraints, like the min days constraint, should only be run once all days are assigned
Optimize Searching with Tree Pruning
- AlphaGo use Monte Caro Tree Search
- We could do something similar to avoid searching dead ends

Conclusion

Given any arbitrary CSP, we can apply fairly naive algorithms, like Backtracking, to find valid solutions. This means we can find solutions to any Sudoku puzzle or Crossword using just a few lines of code.

After some back and forth, I successfully found a holiday on-call schedule that satisfied all requirements. In practice, my coworkers ended up swapping their shifts; proving that even the best algorithm cannot account for the last minute chaos of the holidays.

Useful Links

You can learn more by reading through these links: