Das Math

I just finished re-watching the classic film Das Boot (1981). In this movie, the crew of the U-76, a german U-boat, find themselves in the midst of the WW2 fighting against the allies in the Battle For the Atlantic. The living conditions are claustrophobic and their work is dangerous. What motivates individuals to serve in such perilous conditions? Of course, the answer to this question is obvious to anyone knowledgeable about the history and media surrounding WW2. These advanced machines of war were meant to slip beneath the waves, remain undetected and sink ships.

I had to know more.

How did these crews manage to fling torpedoes at their targets in a world before the digital computer? Well, they used an analog computer!

US Navy Torpedo Data Computer (TDC).
Source: https://en.wikipedia.org/wiki/Torpedo_Data_Computer

Submariners would use complicated electromechanical calculators called TDCs in order to automate the calculations needed to determine how much they need to lead their target. Today, I’d like to go over this problem in detail to share what I’ve learned.

Torpedo Problem

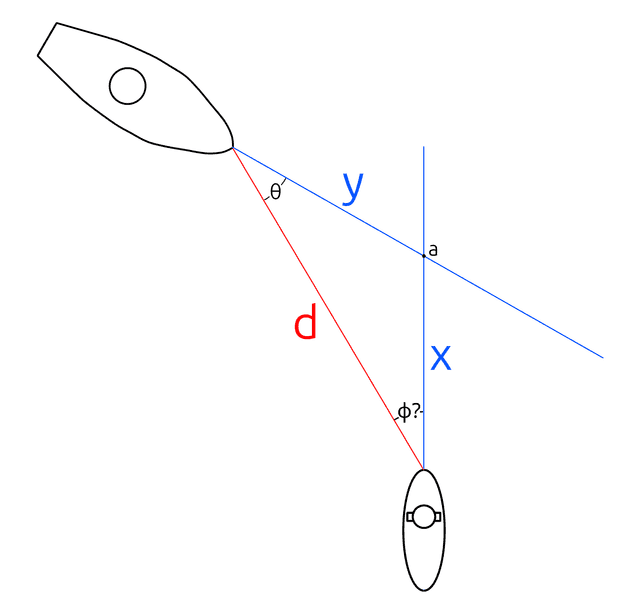
The Torpedo problem is simply what angle should I fire my torpedo such that it will hit the target? We can use the diagram below to better visualize what this looks like.

We know the target boat’s speed $V_s$, and the speed of our torpedo $V_t$. We also know the direction that the target is traveling. Finally we have access to $\theta$, otherwise known as the angle on bow. From just these three numbers, we can determine the angle we need to lead our shot, otherwise known as deflection, we will call this angle $\phi$. When we fire our torpedo, it will travel some distance $x$, while the ship will travel some distance $y$. The torpedo should hit the target at time $T$. Before we can fire our torpedo, let’s break down each component in detail.

Speed

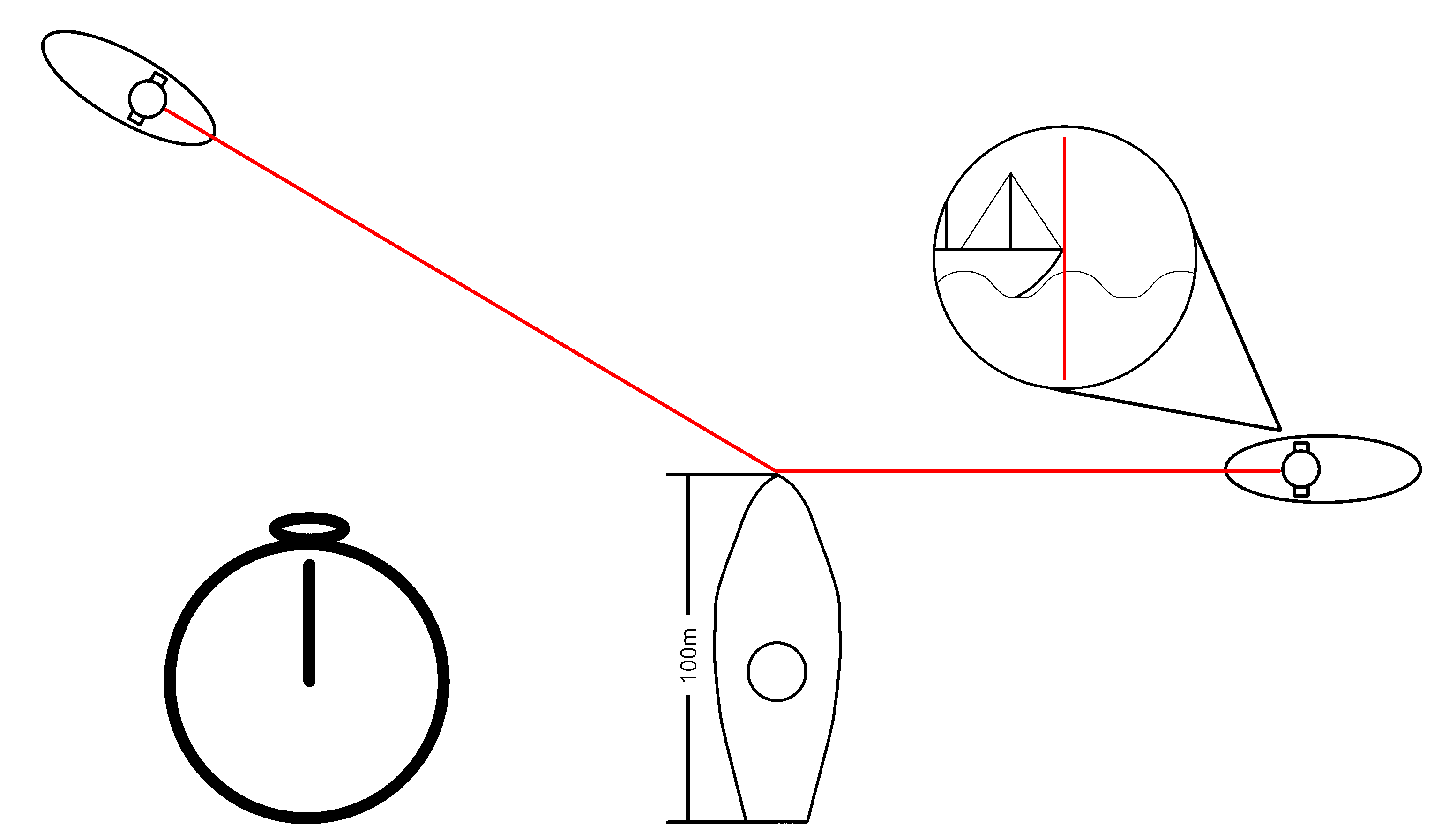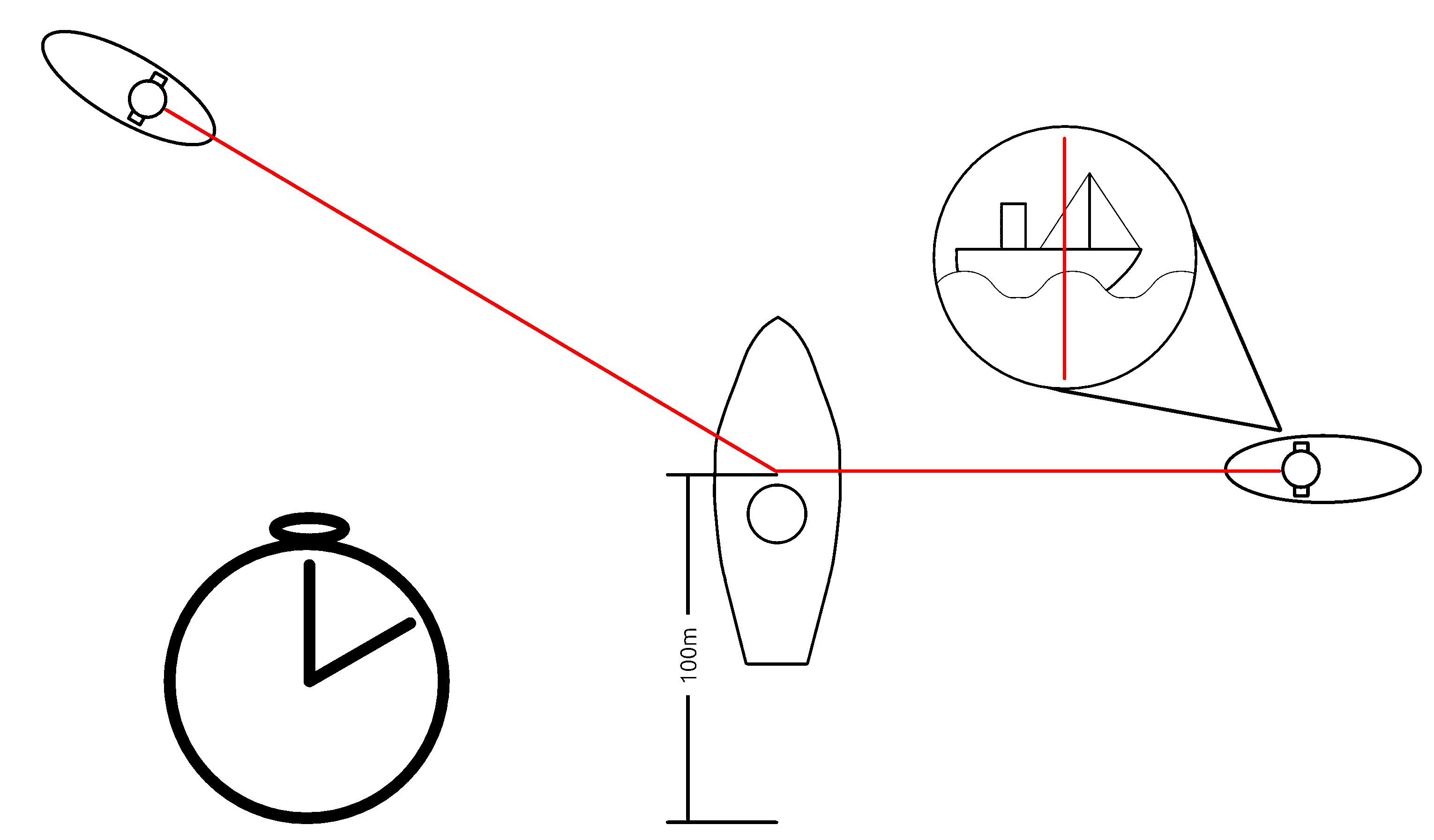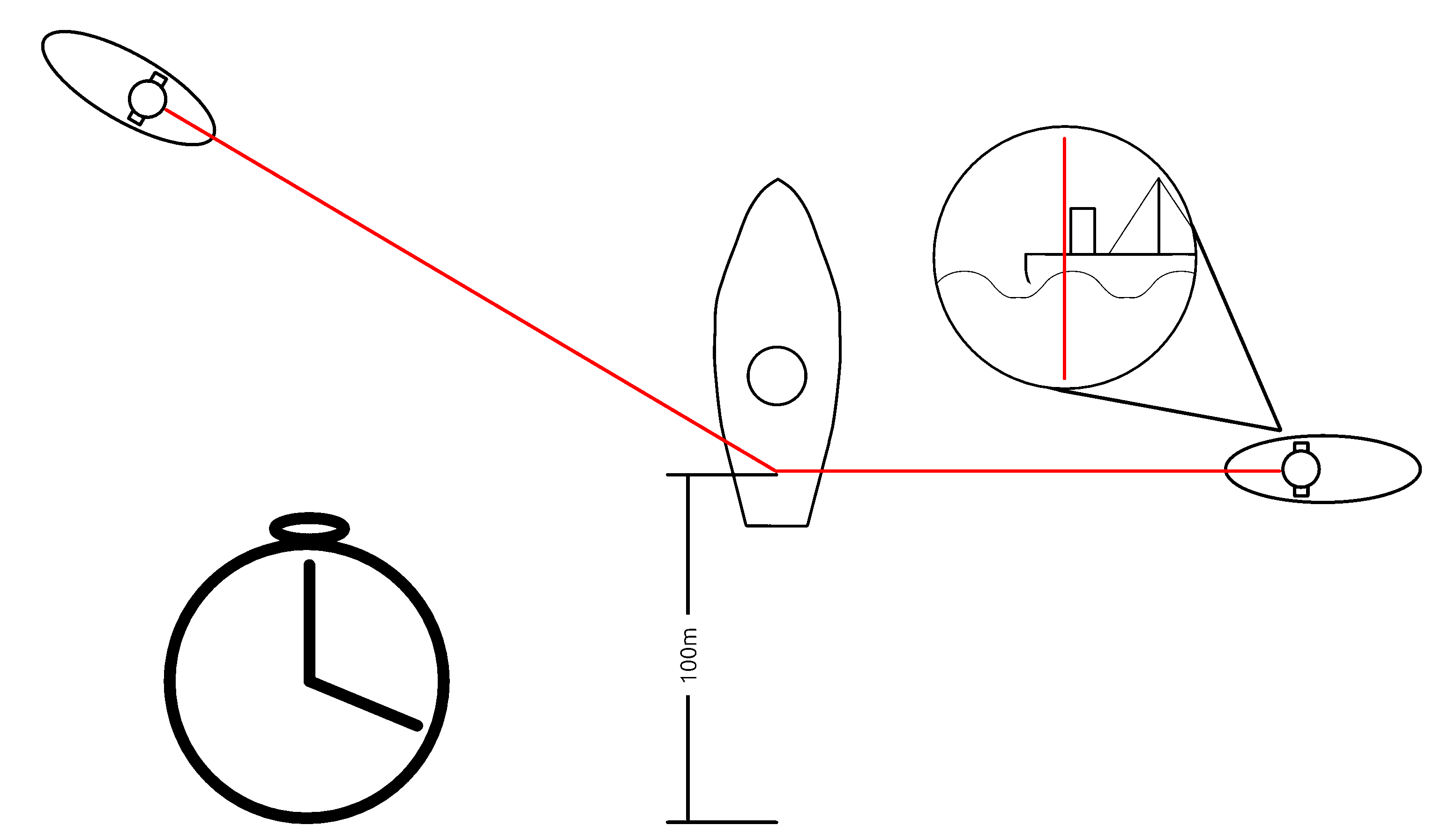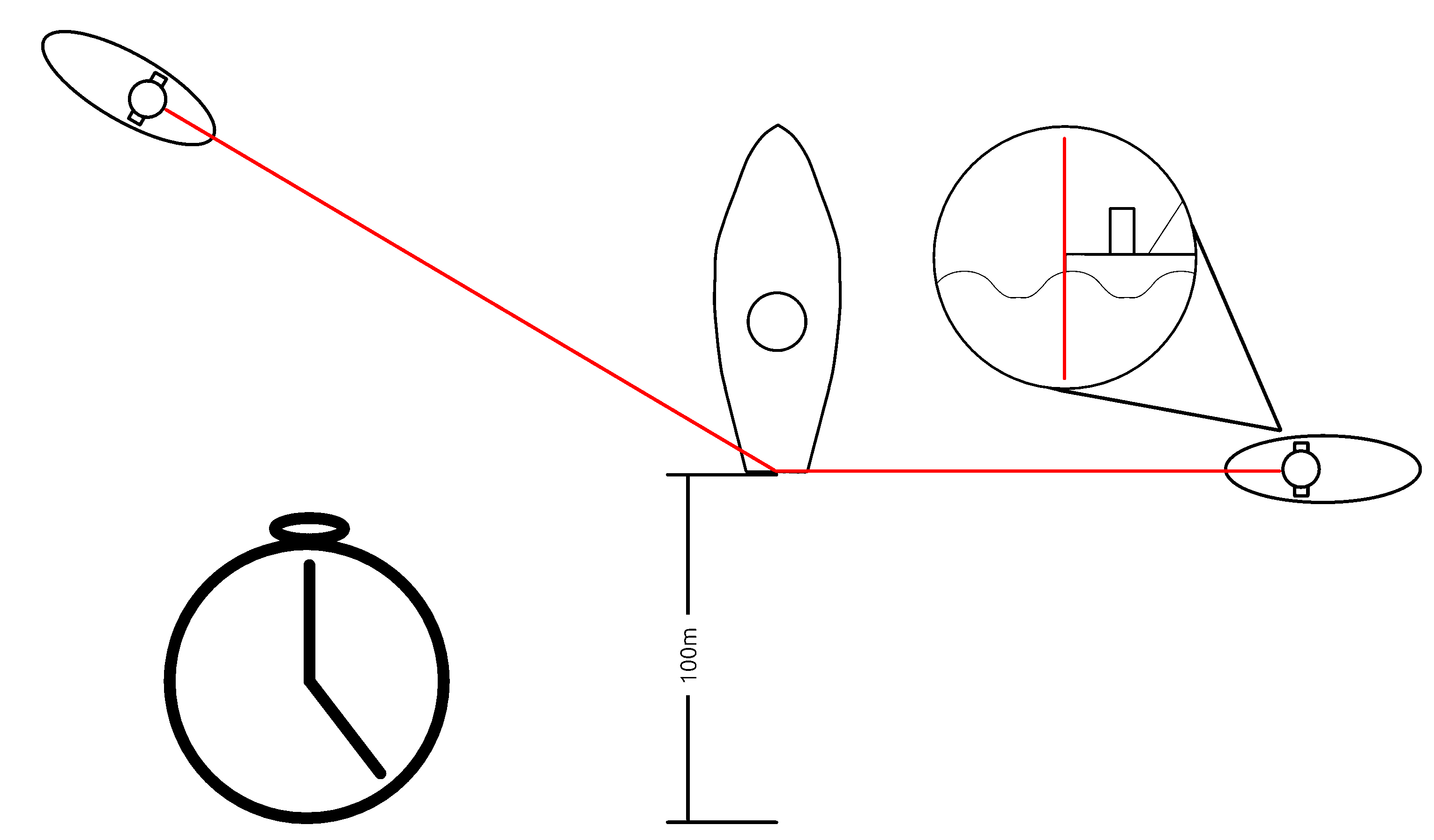
Because we are dealing with the navy, all speeds will be in units of nautical miles (instead of miles) and knots (instead of miles per hour). 1 knot is equal to 1 nautical mile per hour. The way that u-boat captains determine speed is actually quite primitive and fairly easy to understand. If a ship is 100 meters long from the tip of its bow to the back of its stern, and moves at 100 meters/second, then it should take 1 second to travel one length. This is true no matter what angle you observe that ship. If a captain knows the length of a ship, centers his parascope on its bow, and starts a stopwatch, they can observe the ship passing in front of his view. If he stops the stopwatch once the stern passes the cross hairs, he will get the time that it took the ship to move one ship length. Given both the distance traveled, and the time it took, finding the speed is quite trivial. In practice, submariners would have pre-calculated lookup tables that would allow them to take the approximate length and observed time to find the relevant speed in knots ($V_s$). Note that we did not need the distance from our submarine to the target.

Distance

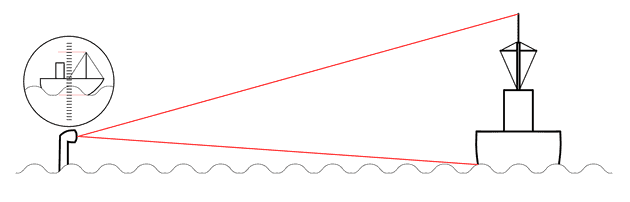
Similarly, telling the distance to the target is also quite easy. Submariners will typically also have prior knowledge of how tall their targets are. By noting how tall the target appears from their view, u-boat captains can use simple trigonometry to determine the distance.

Angle on Bow

Finally, the angle on bow ($\theta$) can often be difficult for people to visualize. The best way to think about it is to imagine you are an observer standing on the bow of the target ship. If you look straight ahead, call that $0^\circ$, the angle you would need to turn your head to see the submarine would be the angle on bow. Sliding back into the u-boat, below is a great visualization of what this looks like from the parascope:

Source: reddit

Putting it Together

So know that we have all this information, let’s revisit the torpedo problem diagram and find our fire solution.

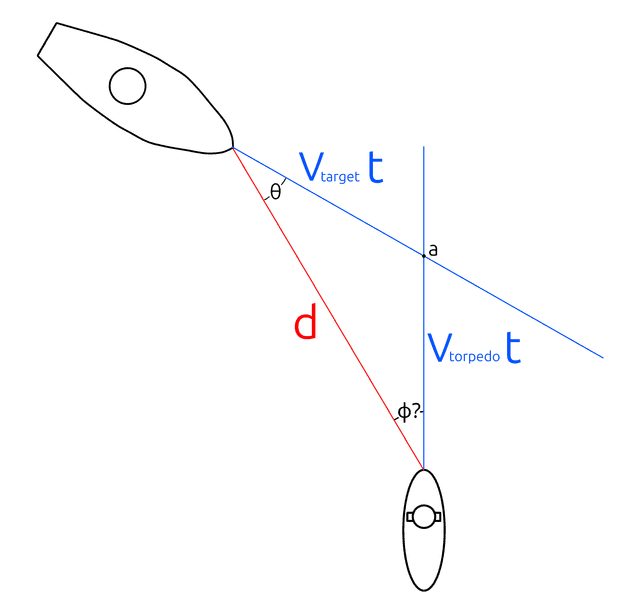
We know the distance to target $d$, the speed of the targeted ship $V_{target}$, the speed of our torpedo $V_{torpedo}$. What we need to find is the angle of deflection $\phi$ that we need to lead our torpedo in order to meet the target ship at some point $a$. One thing that immediately comes to my mind is that the time our torpedo takes to reach $a$ must be the same amount of time that our target takes. If it didn’t, then our torpedo would miss! Let’s call that time $t$. Given that, it should be possible to determine the distance both the torpedo and ship travel to $a$ in terms of $t$.

Now, we can update our diagram to substitute both $x$ and $y$ with the above formulas.

But how can we solve for $\phi$?

Note: I promise that I figured this next part on my own, and only read Wikipedia later.

Law Of Sines

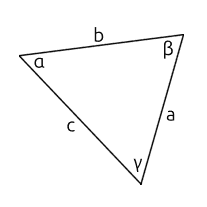
I don’t remember much from high school, mostly by choice, but I do remember learning about the law of sines. Let’s say we have a triangle with three angles $\alpha$, $\beta$, and $\gamma$. It also has three sides $a$, $b$, and $c$.

We can use the law of sines to relate all the angles and sides to each other:

Using this quaint formula, let’s take torpedo diagram:

In order to solve for $\phi$, we set up our law of sines formula ($\alpha$ represents the third unlabled angle). Setting it up:

We can simplify our equation by substituting for our values of $x$ and $y$. $x$ will be $V_{torpedo} \cdot t$ and $y$ of course will be $V_{target} \cdot t$. We will ignore the third team $\frac{d}{\sin(\alpha)}$ since it is unnecessary for our solution.

If we rearrange the above equation, we can begin to see the solution take shape. We can simplify the equation and find the solution!

We finally have a solution for $\phi$! Interestingly, you may have noticed that the time of travel cancels out – it has no influence over the final value. Something else that surprised me when I first derived this equation is that it does not depend on the distance to the target. All that matters is the ratio of the speeds between our torpedo and the target, as well as the angle on bow $\theta$. Just with those three inputs, our torpedo can hit its target. What a terrible power.

Graphing

Now that we have an equation to find our angle of deflection, we can graph the angle on bow $\theta$ vs the how much lead we need to give $\phi$.

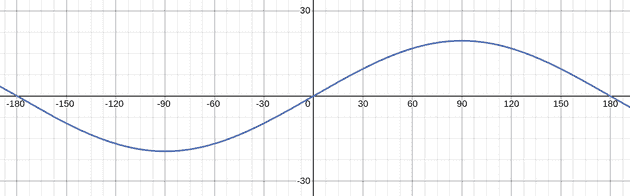
Something fun we can do is play with torpedo speeds, for example, this is the solution for when our torpedo is moving slower than the target ($V_{torpedo}=8$ and $V_{target}=10$).

The above graph shows how when the speed of the torpedo is less than the target, there are conditions in which no firing solution is possible. Unless the target is moving towards us, there is no possible no way the torpedo will make contact.

Conclusion

Today we learned how trigonometry can be deadly. We learned about how submariners can find the distance, speed, and direction of their target. We derived a mathematical formula for determining the firing solution. And we learned how distance is not actually required for that solution. In practice, of course, distance is quite important for submariners. Torpedoes are not all ways accurate, thus it is best to fire them from a close range. Additionally, because a firing solution might be made and adjusted well before a torpedo is fired, knowing the distance allows the TDC to update the angle on bow in real time – circumventing the need to constantly make adjustments to the firing solution manually. Learning about this machines of war has reminded me about how Science and Conflict go hand and hand. As we make an advancement in Math, our ability to shed the blood of our fellow man follows. One day, I hope, we will find ourselves rid of war. In the mean time, as they say in the movie: “ALARM!”