Imagine going to a store, buying eggs, and then making your way home – only to find that those eggs were cracked!
I have relived this exact experience throughout the years. With the price of eggs at an all time high, this is not a mistake I can afford to make. At first, I tried opening the carton of eggs. If any of the eggs are cracked on top, this is a fairly easy test. However, if the eggs are cracked on the bottom, this method will not solve my problem.
Of course, we could spend the time picking up each egg for a closer examination. While this would solve the problem, I would then feel very stupid. At my local grocery store, there is typically a long line of shoppers waiting their turn to retrieve eggs. If one egg takes a second to examine it, a complete examination would require me to hold up the line for a full 12 seconds.
They’d think I was the bad egg!
My Strategy
After thinking about this problem for a while, I eventually decided to develop a heuristic. If I pick three random eggs from the carton, and none of them are broken, I assume that the carton is good. If one of the eggs I pull are broken, then we will consider the carton to be bad. These cartons will then be rejected.
Good cartons have no broken eggs. Bad cartons have broken eggs
Although I’ve been using this strategy for a while, I do not have any way of quantifying its effectiveness. Are there better strategies?
Simulation
In order to evaluate my strategy, I will be using a simulation written in python. For today, good eggs will be modeled as a , while broken eggs will be modeled as a . In this way, we can model a carton of 12 eggs as a list of ones and zeros:
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0]If we assume that any given egg has a X chance of breaking, we can then model all the eggs in the carton using the following:
[1 if (random.random() < X) else 0 for _ in range(eggs_per_carton)]The advantage of this approach is that we can model situations where cartons have multiple broken eggs. In order to evaluate my strategy, we can use the following python code to pull some number of eggs, and check if they are broken:
def strategy_pull_num_eggs(carton, num):
eggs = random.sample(carton, min(num, len(carton)))
# Broken eggs have a value of 1, good eggs are 0
return any([egg > 0 for egg in eggs])Now, all we need to do is run our experiment multiple times in order to determine how accurate our strategy is!
def exec_experiment(epochs=10_000, num_eggs_to_pull=3, gen_method=gen_carton_independent):
# Number of bad cartons found
num_found = 0
# The actual total number of bad cartons
num_with_broken = 0
for _ in range(epochs):
# 1 for broken eggs
# 0 for good eggs
eggs = gen_method()
has_broken_egg = any([egg > 0 for egg in eggs])
if has_broken_egg:
num_with_broken += 1
found_broken_egg = strategy_pull_num_eggs(eggs, num_eggs_to_pull)
if found_broken_egg:
num_found += 1
return epochs, num_with_broken, num_foundGraphs
First Try
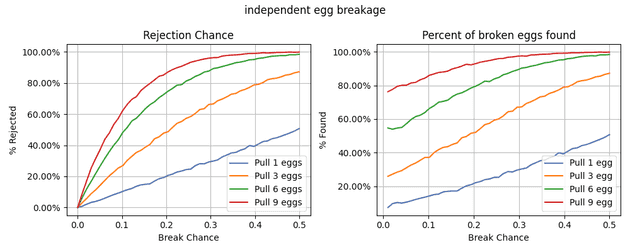
Now that we have simulations, we can graph the results! For each graph, the x-axis represents the probability of any given egg breaking. For the y-axis, The left graphs will show the percent of the egg cartons we decided to reject, while the right graphs will show the percent of bad cartons we rejected. In conjunction, these graphs should be enough to see if our strategy is effective.
Above, we can see how increasing the chance an egg breaks will change the rate our strategy rejects cartons. Off the bat, I am very surprised how ineffective the 3-pull strategy is in the simulation. With a chance of an egg breaking, the 3-pull strategy identifies fewer than of bad cartons, indicating significant room for improvement. I also plotted other numbers of pulled eggs to compare. Unsurprisingly, pulling 9 eggs will fare much better at finding bad cartons. Similarly, if we only pull 1 egg, our test will perform poorly.
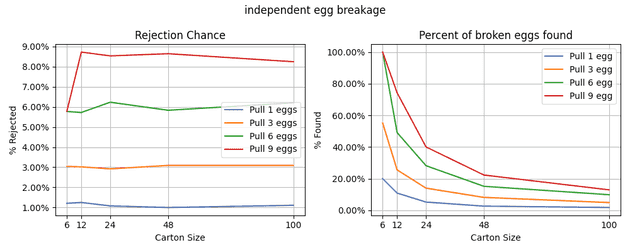
Another interesting factor I wanted to investigate was how the size of the carton affected my strategy. While I typically purchased a dozen eggs, there are other sizes that eggs can be purchased in. These simulations pin the egg break chance at . I decided on using my experience and intuition - otherwise the number is fairly arbitrary.
Looking at the right graph, we can see how our strategy fails. The pull strategy works well for small cartons but becomes less effective as carton size grows. We’d need to start using pull sizes in the dozens to find bad cartons.
Further, it also seems like the carton size will not affect our rejection rate. This can be seen in the left graph. What must be noted in these graphs is that since the chance any egg breaks is independent of the size of the carton, as the carton size increases, so should the chance that the carton is bad. It’s highly likely that in a carton of 50 eggs, that at least one of those eggs is bad. This may be a disadvantage of the model I chose to use.
This time with dependent breaks
So far, my strategy seems ineffective. This is not a scalable way to find broken eggs. However, my simulation assumes that eggs break independently from each other. This is not an accurate assumption.
If a carton of eggs experiences a shock powerful enough to break one egg, the odds are high that neighboring eggs will also break. This is known as dependent probabilities. For example, the odds that it is raining outside and the ground is muddy depend on each other. If we know it is raining, we’d probably say it was also muddy. Likewise, if one egg in a carton is broken, we’d assume that some nearby egg would be as well.
We can model this by first breaking eggs with our independent probability. Iterating through the list, if we find a broken egg, we can then use a collateral probability to determine if the neighboring eggs in the list should also break. If we perform this calculation multiple times, we can then model cartons more realistically.
def gen_carton_dependent(eggs_per_carton=12, chance_broken_egg=0.01, collateral_prob=0.5, num_rounds=3):
# One broken egg, means we will likely have more broken eggs
eggs = [1 if (random.random() < chance_broken_egg) else 0 for _ in range(eggs_per_carton)]
new_eggs = eggs[:]
# For each round of running:
for _ in range(num_rounds):
for i in range(len(eggs)):
if eggs[i] == 1: # Check for a `1`
# Check left neighbor
if i > 0 and eggs[i - 1] == 0:
if random.random() < collateral_prob:
new_eggs[i - 1] = 1
# Check right neighbor
if i < len(eggs) - 1 and eggs[i + 1] == 0:
if random.random() < collateral_prob:
new_eggs[i + 1] = 1
eggs = new_eggs
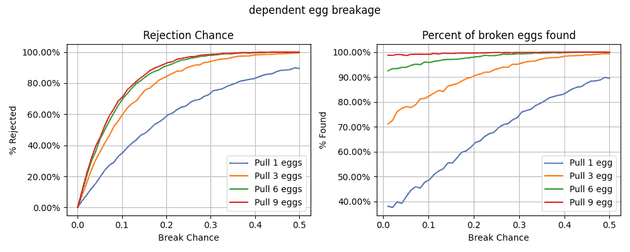
return eggsThe important observation here to make is that while the number of broken eggs will increase, the percent of bad cartons will not. Thus, the number of broken eggs per bad cartons will increase.
This graph looks much better! Since cartons will have more broken eggs on average, small sample sizes will still result in an effective test. In fact, pulling three eggs should find more than 70% of bad cartons. Further, a 9-pull or even a 6-pull strategy will give near certain results.
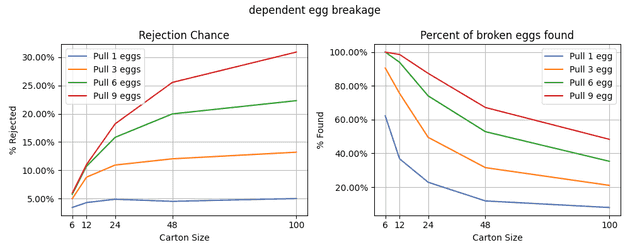
Unlike in the independent egg breakage model, our test is also more effective for larger carton sizes. Still, the approach does not scale well with larger sizes. This can be seen how in the right graph, the percent of bad cartons found will decrease. Even if, as we see in the left graph, the percent of cartons rejected increases, we cannot keep up with the scale of the carton size.
Conclusion
In conclusion, I have written a simulation for determining if a carton of eggs has any cracks or leaks. Assuming that you don’t immediately notice a broken egg when you open the carton, examining a sample of the eggs more closely should be an effective strategy.
If we assume that one broken egg is likely to be near other broken eggs, then my 3-pull strategy will be fairly effective. Given my assumptions, and an egg break chance of , I should be able to identify of bad cartons while only rejecting ~ of cartons. If you want a near certainty that none of your eggs are broken, my simulations recommend pulling 6 of the eggs. Although I will continue using my 3-pull strategy.
However, this strategy does not scale well with larger carton sizes. The chance of a random one-off broken egg is too large to be able to find it with only a handful of sample eggs. Either my assumptions in this simulation are wrong, or I will need to identify a new test when buying eggs in bulk.
If you have a better strategy, I would love to know! The code I used in this post is available on Github if you are interested.