Simulating Spaceships at Light Speed

Most of us have a rough idea that relativity affects space travel, but the details can feel abstract. I know I didn’t fully grasp it. So, on a whim, I decided to build a basic simulation to visualize how different observers would perceive a spaceship traveling near light speed.

What Is Relativity?

We all know the cosmic speed limit: light travels at $c$, about $299,792,458$ meters per second. But what does that really mean?

Einstein realized something fascinating: the speed of light is constant for all observers, no matter their motion.

Imagine you’re stationary on Earth. You turn on a flashlight and measure those photons zipping away at exactly $c$. But if you were flying in a spaceship at $25$ the speed of light and turned on that same flashlight, you’d still measure the photons traveling at $c$.

Okay, but what if I were floating in space watching you whiz by at 75 million meters per second? If I measure the light leaving your flashlight, I still get $c$.

By contrast, if you fired a bullet at me, I’d measure the bullet’s speed roughly as 75 million + 1,000 meters per second (technically it’s more complicated, but close enough¹). But light? Always $c$.

That’s the heart of relativity: no matter your speed, every observer measures light at the same speed.

The Implications

How can this be? Einstein explained that the universe balances two effects:

Time Dilation: Time slows down for people aboard fast-moving ships². From your perspective on the ship, the universe outside seems to speed up. With a good enough telescope, you might watch a baby grow into adulthood in minutes.

Length Contraction: Space compresses in the direction of your motion. Distances that seem vast to people on Earth shrink dramatically for you. From your perspective, your destination rushes toward you faster than expected - sometimes appearing to exceed light speed, an effect called celerity³.

These two effects perfectly balance to ensure all observers measure light traveling at $c$. The Math Behind the Simulation

To simulate this, I used rapidity⁴, a mathematical tool that simplifies adding velocities under relativity.

Given a rapidity $\theta$, we convert to velocity (from Earth’s perspective):

Meanwhile, the astronaut aboard the ship experiences proper velocity, or celerity:

Notice that the velocity that the ship experiences might not equal the velocity someone on Earth might measure. Initially, $\theta$ is zero (at rest). When the ship accelerates at $a$ for a duration $\Delta \tau$ (proper time on the ship), rapidity increases:

The updated rapidity becomes:

We can then compute how far the ship moves:

Finally, to relate ship time to Earth time:

Thus, for every moment aboard the ship, Earth experiences a different amount of time.

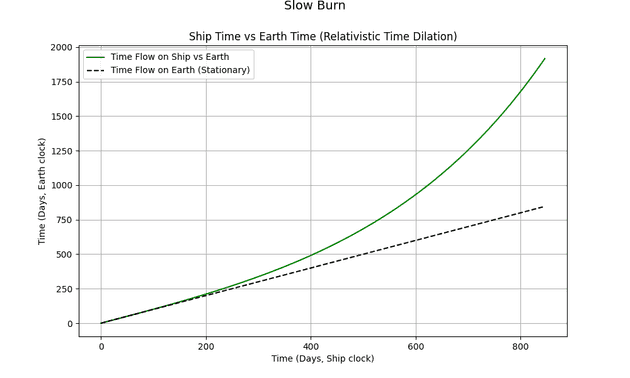
In Practice

In the graph above, we simulate a ship accelerating at $1g$ continuously. The x-axis shows time aboard the ship; the y-axis shows Earth time. As speed increases, Earth time stretches dramatically compared to the ship’s clock.

Brachistochrone Trajectory

For interstellar travel, the fastest path is the Brachistochrone trajectory; burn your engines halfway toward your destination, then flip and burn to slow down¹.

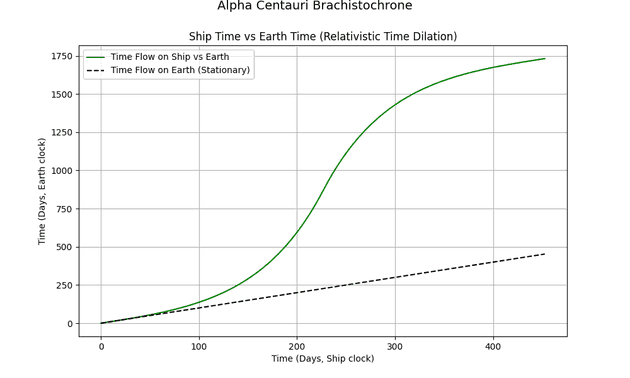
Using my simulation (code on GitHub), I explored this in detail. First, let’s compare time aboard the ship and back on Earth:

The ship accelerates for 250 days, then decelerates. During acceleration, Earth time flies by compared to ship time. As deceleration begins, the clocks drift back toward syncing.

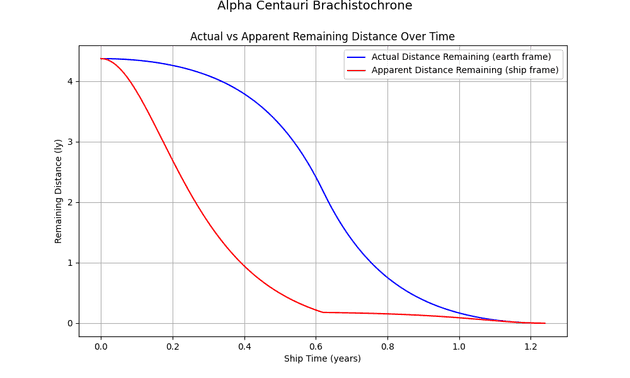
We can also visualize distance from each perspective:

To an Earth observer, the ship speeds up, turns, and slows as it nears the star. But to those aboard the ship, the destination rapidly “contracts” - appearing almost within reach halfway through the trip.

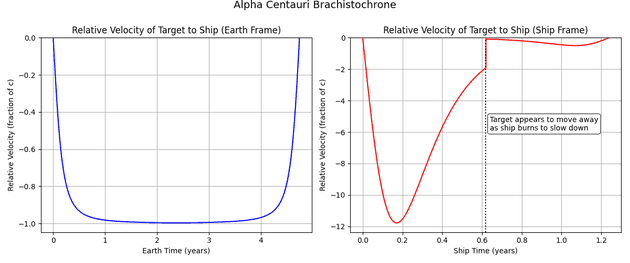
Velocity perceptions differ too:

On the left, Earth sees the ship nearing (but not exceeding) $c$. On the right, the ship’s crew witnesses strange phenomena:

• After months of acceleration, their proper velocity surpasses $c$ (not a violation of physics - it’s an effect of time dilation and length contraction).

• At the halfway mark, distance appears nearly gone.

• During deceleration, space stretches, and the destination appears to recede, even as the ship moves forward.

Visualizing the trip

Putting this together, we can visualize the trip from both Earth and the Spaceship:

Red hexagon = spaceship
Blue circle = Earth
Green circle = destination (Alpha Centauri planet)
Orange triangle = engine exhaust (acceleration/deceleration)
Clock = time dilation experienced by Earth, ship, and destination

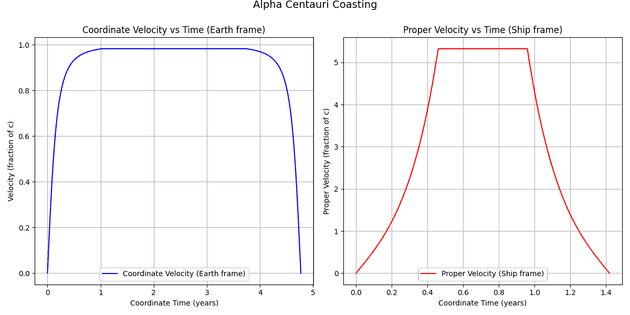
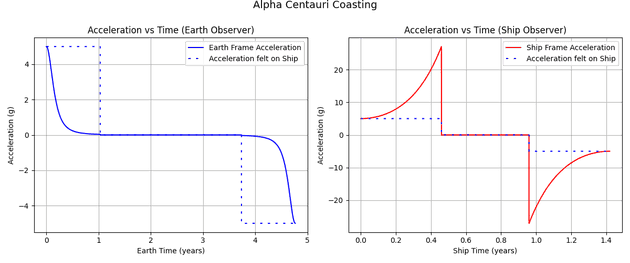
Coasting Trajectory

Not every mission prioritizes speed. Fuel limits often demand long coasting periods between brief acceleration phases.

During coasting, ship speed remains constant, but time dilation distorts perceived durations differently for ship and Earth observers.

An Earth observer sees acceleration drop near light speed, despite the ship applying steady thrust. Conversely, the ship’s crew perceives exaggerated acceleration - a byproduct of relativistic distortions.

Finally, let’s observe these coasting trajectories from both the Earth and the spaceship:

Conclusion

Relativity transforms space travel into something truly alien to our everyday experiences. Time, distance, and even velocity become flexible, observer-dependent concepts once you approach light speed.

These simulations, while simplified, reveal the strange beauty of high-speed space flight - from apparent faster-than-light journeys to time itself stretching and contracting depending on your frame of reference.

Exploring these effects isn’t just academic - it’s essential for anyone dreaming of humanity’s first real steps to the stars.

All code used for this project is available on github: https://github.com/cwlowder/blog-post-code/tree/main/relative-brachistochrone